Die Mathematik ist nicht nur die Sprache, in der man die Grundgesetze der Physik formuliert sowie andere Gesetze daraus ableitet. Sie ist auch die Sprache, in der man zu neuen Hypothesen und Einsichten über die Natur gelangt, die zumindest prinzipiell der experimentellen Überprüfung zugänglich sind.
Auf einen weiteren Aspekt der mathematischen Naturbeschreibung möchte ich nun hinweisen. Gewöhnlich beschreiben wir die Welt mit Begriffen, die in uns so etwas wie „Bilder“ assoziieren. Diese „Bilder“ entstammen unserer Erfahrung aus einer „mittleren“ Welt, deren typische Skalen sich in Millimeter bis Kilometer messen lassen. Diese „Bilder“ verwenden wir aber auch, wenn wir z. B. gedanklich in die Mikrowelt vorstoßen, in dem wir uns Atome, aber auch Elementarteilchen, als kleine Kugeln vorstellen. Gewöhnlich hält ein Nichtphysiker dieses „Bild“ sogar als reale, adäquate Vorstellung von Mikroobjekten. Das ist aber nicht der Fall, wie uns die Quantenmechanik lehrt. Mit Vorstellungen aus der Welt der mittleren Skalen kommt man hier nicht weit, wenn es um Superposition, Verschränkung oder Welle-Teilchen-Dualismus geht. Hier benötigt man völlig neue Strukturen und Begrifflichkeiten, die weitab unseres normalen Vorstellungsvermögens liegen. Sie entstammen wiederum der abstrakten Mathematik (man denke an die Abstraktion des Hilbert-Raumes oder der Wellenfunktion) und sie helfen uns, dass wir uns auch in der Welt der Quanten in völliger logischer Klarheit bewegen können. Die Mathematik erweist sich in diesem Zusammenhang als die tauglichste Sprache im Bereich des für den Menschen Unvorstellbaren.
Doch nun noch ein paar Worte zu den „Axiomen“, die als Grundlage für eine mathematische Theorie (hier der Geometrie der Ebene) vor etwa 2300 Jahren der berühmte griechische Mathematiker Euklid eingeführt hat. Seine „Elemente“ gelten auch heute noch als eine mustergültige mathematische Theorie, an der besonders erstaunt, wie sich mit wenigen Grundannahmen ein hervorragend funktionierendes mathematisches Modell entwickeln lässt, welches mit großer Exaktheit die Geometrie unsere Welt beschreibt. Das Wesen der axiomatischen Methode lässt sich vielleicht am besten erkennen, wenn man „Axiome“ mit „Spielregeln“ übersetzt. Das Schachspiel ist dann ein Spiel, welches auf ein für alle Mal festgelegten Spielregeln beruht, die weder in Frage gestellt werden, noch deren Ursprung weiter hinterfragt wird. Vielmehr werden von den Spielern gewaltige Anstrengungen unternommen um zu ergründen, ob man unter exakter Einhaltung dieser Regeln in einer speziellen Spielsituation das Spiel gewinnen kann. Also im Prinzip die gleiche Methode, die ein Mathematiker oder theoretische Physiker anwendet, der am Ende wissen möchte, ob sich mit dem verwendeten Axiomensystem (oder der physikalischen Theorie) ein gerade interessierendes Problem lösen lässt oder nicht.
Die Idee übrigens, dass jede mathematische Theorie auf Axiomen beruhen sollte, geht auf David Hilbert (1862-1943) zurück. Er war der Meinung, dass sich jeder mathematischen Aussage, die innerhalb eines widerspruchsfreien Axiomensystems formuliert werden kann, das Prädikat „wahr“ oder „falsch“ zuordnen lässt. Aber so ist es interessanterweise nicht, wie der geniale Logiker Kurt Gödel (1906-1978) im Jahre 1931 bewiesen hat (Sie kennen vielleicht „Gödels Theorem, Sumpf, Pferd und Schopf…“). Er wies nämlich in seinen berühmten Unvollständigkeitssätzen nach, dass man in einer axiomatisch aufgebauten Theorie immer Aussagen finden kann, deren Wahrheitswert innerhalb des Systems nicht feststellbar ist. Auch gibt es - beispielsweise in der Arithmetik - mathematische Sätze, die zwar wahr sind, deren Wahrheitswert sich aber innerhalb des Axiomensystems prinzipiell nicht beweisen lässt. Mittlerweile konnten übrigens Mathematiker schon einige Aussagen finden, die sich in den entsprechenden Axiomensystemen nicht beweisen lassen.
Wer sich die Mühe machen möchte, die Gödelschen Sätze und ihre Implikationen zu verstehen, dem sei das Kultbuch von Douglas R. Hofstädter „Gödel, Escher, Bach - ein Endloses Geflochtenes Band“ ans Herz gelegt. Darin lernt man u. a., dass die geniale Entdeckung Kurt Gödels nicht nur in der Mathematik von Bedeutung, sondern von allgemeiner Natur ist. Kernpunkte sind dabei Aussagen, die so etwas wie eine Selbstbezüglichkeit aufweisen und deshalb zu semantischen Paradoxien der Art „Alles, was ich sage, ist Lüge“, führen.
Der nicht immer einfache, aber wahrlich durchkomponierte Text wird dabei durch die Grafiken des niederländischen Grafikers Maurits Cornelis Escher (1898-1972) aufgelockert, auf die auch im Text immer wieder eingegangen wird. Auch sie sind hochgradig paradox, denn sie stellen entweder Unmöglichkeiten (man denke an die Grafiken „Treppauf, Treppab“ und „Wasserfall“) oder erstaunliche Flächenparkettierungen (z. B. „Metamorphosis I“ oder „Day and Night“, sogenannte Escherkacheln) dar. Bemerkenswert ist auch Eschers Versuch, die "Unendlichkeit" bildhaft darzustellen. Er fand, ausgehend von seinen Parkettierungen, zwei Lösungen dafür. Die eine besteht darin, von der Ebene zu einer randlosen Fläche überzugehen und die andere in der Verwendung nichteuklidischer Geometrien, wie sie z. B. von dem russischen Mathematiker Nikolai Iwanowitsch Lobatschewski (1792-1856) entwickelt wurden. Auf diese Weise sind übrigens seine berühmten Schlangen- und Fischmotive entstanden. Escher ist weiterhin auch ein gutes Beispiel dafür, wie sich Mathematik und Kunst gegenseitig befruchten können. Denn selbst Formeln, die einem normalen Betrachter trocken und nichtssagend vorkommen, können bei einem Kenner der Materie durchaus einen eigenen ästhetischen Reiz entwickeln.
Das Paradebeispiel dafür ist die von Leonhard Euler 1748 entdeckte Beziehung
Sie verknüpft zwei transzendente Zahlen, nämlich die Eulersche Zahl e (die Basis der natürlichen Logarithmen) mit der Zahl Pi, dem Verhältnis von Kreisumfang zu dessen Durchmesser mit der Wurzel aus (-1) (= der imaginären Einheit i) zu einem Wert -1. Und das ist wirklich so, wie sich leicht beweisen lässt. Trotzdem ist es irgendwie erstaunlich und geheimnisvoll, wie zwei Zahlen, die sich nicht mal als Brüche darstellen lassen und bei der die eine für „exponentielles Wachstum“ und die andere mit allem, was mit Kreisen zu tun hat, zuständig ist, zusammen mit der „unmöglichen Zahl“ (Wurzel aus (-1)) genau -1 ergibt (der Mathematiker nennt das „Eulersche Identität“).
Apropos „exponentielles Wachstum“. Erinnern Sie sich noch an den Club of Rome? Dieser 1968 gegründete und ziemlich elitäre Verein wurde 1972 bekannt, als er die Studie „Grenzen des Wachstuns“ veröffentlichte. Darin versuchten die Autoren zu zeigen, dass ein ungebremstes Wachstum der Bevölkerung, der Industrialisierung und des ökologischen Raubbaus irgendwann an seine natürlichen Grenzen (Ressourcenmangel) stoßen und sich zu einer globalen humanitären Katastrophe entwickeln muss. Die Begründung erfolgte dabei sehr einsichtig mit der Dynamik exponentieller Wachstumsprozesse. Die zeitlichen Vorhersagen jedoch, die in dieser ersten Studie gemacht wurden, erwiesen sich allesamt als falsch, während die angewandte Methodik - Simulation zukünftiger Entwicklungen auf der Grundlage der Systemtheorie - im Laufe der folgenden Jahrzehnte immer mehr verfeinert wurde. Der letzte Bericht stammt übrigens aus dem Jahre 2012 und trägt den Titel „2052: A Global Forecast for the Next Forty Years“. Ihn kann man durchaus sowohl inhaltlich als auch methodisch als seriös betrachten und als politische Handlungsanweisung für die nächste Zukunft in Betracht ziehen. Natürlich krankt auch er an dem Problem, welches der Überlieferung nach keiner so passend und prägend wie Karl Valentin (1882-1948) formuliert hat:
„Prognosen sind schwierig, besonders wenn sie die Zukunft betreffen“
(dieser Ausspruch wird manchmal auch Niels Bohr zugeschrieben). Aber kommen wir zum Kernpunkt zurück, dem exponentiellen Wachstum. Was es eigentlich bedeutet, können sich die meisten kaum vorstellen. Ansonsten würden sie sich an solchem Quatsch wie Kettenbriefe und anderen Schneeballsystemen kaum beteiligen.
Dazu folgende einsichtige Legende mit überraschendem Ergebnis: Der Erfinder des Schachspiels konnte mit seinem Spiel seinen König derartig begeistern, dass dieser ihm einen Wunsch gewährte. Und dessen Wunsch klang anfänglich ziemlich harmlos. Der Erfinder des Schachspiels wünschte sich also eine Menge Reiskörner, wobei sich deren Anzahl aus einer einfachen Regel ergibt - und zwar wie folgt: Ein Korn solle auf das erste Feld, zwei auf das zweite, vier auf das dritte, usw. gelegt werden (d.h. auf einem Feld immer doppelt so viele Reiskörner wie auf dem vorangehenden) bis alle 64 Spielfelder abgearbeitet sind. Dem König kam dieser Wunsch ziemlich bescheiden vor, so dass er ihm ohne viel nachzudenken versprach, der Bitte nachzukommen. Als nun der Hofmathematiker begann, die Menge der Reiskörner auszurechnen, wurde die Monstrosität des "bescheidenen" Wunsches schnell klar. Also rechnen wir: 1+2+4+8+16+32+...+2^64 = 18446744073709551615. Das sind rund 1.8∙10^19 Reiskörner. Wenn also ein Reiskorn 0,03 Gramm wiegt, dann wiegen 1.8∙10^19 Reiskörner 5.5∙10^11 Tonnen, also 550 Milliarden Tonnen. Das entspricht rund 1150 weltweiten Reisernten (Stand 2014). Würde man, grob gerechnet, alle diese Reiskörner gleichmäßig auf die Fläche Deutschlands verteilen, dann ergäbe sich eine Schichtdicke von etwa einem viertel Meter. Und dabei haben wir es hier nur mit einer einfachen geometrischen Reihe zu tun. In die Kategorie „exponentielles Wachstums“ fällt u. a. auch die Bakterienvermehrung (ein Bakterium teilt sich alle halbe Stunde), die Bevölkerungsexplosion (siehe Thomas Robert Maltus (1766-1834) „The Principle of Population“) und die Rohstoffgewinnung (man denke nur an eine unregulierte Ausbeutung von Ölvorkommen).
Alle diese „Wachstumsarten“ haben die Eigenschaft, dass sie begrenzt sind, da sie Ressourcen verbrauchen - und die hier zu betrachtenden Ressourcen sind nun einmal alle endlich. So begrenzen die natürlichen Ressourcen der Erde - wie der Club of Rome richtig feststellt - die maximale Zahl an Menschen, denen bei einem gewissen Wohlstand eine Ernährung gesichert werden kann. Diese Zahl dürfte irgendwo bei 8 Milliarden liegen - ein Wert, der bis zum Jahr 2030 erreicht sein wird. Aus ökologischen Gründen ist aber selbst dieser Wert zu hoch. Unsere Erde ist eigentlich nur für 500 Millionen bis 1 Milliarde Menschen gemacht. Jede Zahl, die größer ist, führt mittel- und langfristig zu Problemen, wobei keiner weiß, ob, und wenn ja, wie sie sich bewältigen lassen.
Diese Erkenntnis folgt aus Untersuchungen, welche die sogenannten „Planetaren Grenzen“ in Bezug auf neun ausgewählte Parameter aufzeigen – und, methodisch ähnlich, in dem man, wiederum auf eine Auswahl von Parametern bezogen, die „Fläche“, die ein Erdenbürger in Hektar für seinen Lebenserhalt benötigt, berechnet und als dessen „Ökologischen Fußabdruck“ ausweist. Aber alle diese Untersuchungen haben nur einen akademischen Wert, wenn sie nicht zu politisch umsetzbaren Maßnahmen führen. Und hier ist nach allen Erfahrungen Skepsis angesagt. Das „Raumschiff Erde“ hat viele Kapitäne, jedoch keinen Steuermann und die Besatzung platzt aus allen Nähten. In den meisten Kabinen herrscht bittere Armut und in einigen regieren Mord und Totschlag. Dass es uns trotzdem so komfortabel vorkommt, ist nur der Tatsache geschuldet, das wir nicht im Slum einer Großstadt der Dritten Welt leben – wie ein Großteil der Menschen auf der Erde. Aber der Geschützdonner nähert sich, wie man feststellen kann, wenn man mit Aufmerksamkeit die täglichen Nachrichten verfolgt. Das Gebot der Stunde ist es, wenn man sich die Zahlen des Bevölkerungswachstums außerhalb der Industriestaaten ansieht, die Bevölkerungsexplosion human zu verlangsamen. Die Korrelationen, die einen Lösungsweg aus diesem Dilemma bieten, sind schon lange bekannt: Mehr Bildung, bessere Ausbildung und Chancengleichheit auch für Frauen, eine gezielte Familienplanung unter Zurverfügungstellung der dazu notwendigen Hilfsmittel, eine vernünftige Gesundheitsvorsorge und etwas mehr Komfort und Sicherheit im Leben lässt (wie die Industrienationen überdeutlich zeigen) die Geburtenrate purzeln. Aber das ist alles leichter gesagt als getan. Und die Bedingungen, solch ein Programm durchzusetzen, scheinen sich auch eher zu verschlechtern, wenn man die vielen Konfliktregionen der Erde mit in Betracht zieht. Aber mit etwas Glück und Verstand folgt uns, die wir noch im Paradies leben, nur das Fegefeuer und nicht die Hölle auf dem Weg zu den Sternen. Denn die Natur wird einen Weg finden, das Problem einer Übervölkerung zu lösen. Die mathematische Formel, an die sich die Natur in dieser Beziehung halten wird und welche die Entwicklung einer Population von Lebewesen bei begrenzten Ressourcen mit der Zeit beschreibt, ist übrigens seit 1845 bekannt.
Sie wurde bei einer Analyse der Maltusschen Theorie des Bevölkerungswachstums durch den Mathematiker Pierre François Verhulst (1804-1849) entdeckt. Diese „Verhulst-Gleichung“ ist im deutschsprachigen Raum mehr unter dem Namen „Logistische Gleichung“ bekannt. In der zweiten Hälfte des 20. Jahrhundert wurde sie detailliert untersucht, da sie eng mit dynamischen Systemen, welche zu chaotischen Zuständen neigen, in Beziehung steht. Wie sie funktioniert, soll folgendes Beispiel zeigen. Es geht hier um die Nonne. Nein, nicht die im Kloster, sondern um den Schmetterling Lymantria monacha, dessen Raupen in früheren Zeiten innerhalb kürzester Zeit ganze Nadelwälder (die Ressource, von der sie zehren) kahlgefressen haben. Heute bringt man diesen Schmetterling aus der Familie der Spinner mit Gift um, wenn es nach Meinung der Forstleute notwendig sein sollte. Deshalb ist er nicht mehr so oft zu sehen wie früher.
Der Lebenszyklus dieses Nachtfalters sieht wie folgt aus: Die weiblichen Falter legen im Spätsommer ihre Eier ab, aus der dann im Frühjahr die Raupen schlüpfen. Sie machen sich dann sofort über Fichten- und Kiefernadeln her, bis sie rund 1000 Fichten- oder 300 Kiefernadeln verputzt haben. Dann sind sie ausgewachsen und suchen sich ein lauschiges Plätzchen, wo sie sich einen Kokon spinnen und darin verpuppen. Zwei, drei Wochen später schlüpfen daraus nach vollzogener Metamorphose die Nonnenfalter. Sie paaren sich, legen Eier auf die Stämme von Nadelbäumen und sterben ab. Aber mit den Eiern, die überwintern, beginnt das jährliche Spiel von neuem. Nun kann man sich vorstellen, dass sich eine Ausgangspopulation dieses Insekts jedes Jahr verdoppelt - so wie die Reiskörner auf dem Schachbrett. Andernfalls gibt es aber auch Prozesse, die diesem Populationswachstum entgegenwirken, wie Fressfeinde, Witterung, Parasiten oder die endliche Zahl von Nadeln in einem Nadelwald. Mathematisch lässt sich solch ein Szenario am besten über Populationsverhältnisse, das heißt, durch den Quotienten aus der Populationsgröße X(n+1) im Jahr n+1 zur Populationsgröße X(n) im Jahr n beschreiben, wobei noch eine Normierung derart durchgeführt wird, dass die jeweils größtmögliche Population gleich 1 (oder gleich 100%) gesetzt wird. Einfaches exponentielles Wachstum lässt sich dann formal mittels der Rekursionsformel X(n+1)=K X(n) beschreiben, wobei K eine zu wählende Konstante ist und die sich als „Geburtenrate“ interpretieren lässt. Die Idee von Verhulst war es nun, diese einfache Beziehung um einen weiteren Faktor auf der rechten Seite zu ergänzen, welche die dem Wachstum entgegenstehenden Prozesse formalisiert: X(n+1)=K X(n) (1-X(n)). Und ihre Wirkung ist leicht zu erkennen. Für einen sehr kleinen Wert von X(n) liegt (1-X(n)) nahe bei 1, so dass die Gleichung sich nicht allzu sehr von der ursprünglichen Wachstumsgleichung unterscheidet. Wenn X(n) jedoch sehr groß wird, dann marschiert der Faktor (1-X(n)) gegen Null und sorgt dafür, dass im Grenzfall die rechte Seite verschwindet. Offensichtlich arbeiten beide Terme gegeneinander. Der erste Term versucht, die Population immer mehr zu vergrößern während der zweite Term dieses ungezügelte Wachstum unterdrückt. Man hat es hier offensichtlich mit einer nichtlinearen Rückkopplung zu tun, und gerade das macht die Verhulst-Gleichung allein für sich schon äußerst interessant. Man kann nun leicht mit einem Computer untersuchen, wie sich eine Ausgangspopulation im Laufe der Jahre bei unterschiedlichen Geburtenraten K entwickelt. Liegt z. B. die Geburtenrate unterhalb von 1 (wie bei uns in Deutschland, 1 bedeutet hier einfache Reproduktionsrate), dann wird die entsprechende Population über kurz oder lang aussterben. Bei einer Geburtenrate von K=1,5 führen beide Richtungen, egal ob man mit einer Population von 100% oder mit einer kleinen Population von 1% der möglichen 100% beginnt, zu einem stabilen Grenzwert, der bei ~66% liegt. Hier stabilisiert sich die Populationsentwicklung und ändert sich in den folgenden Jahren nicht mehr. Erhöht man den K-Wert weiter, z. B. auf 2,5, dann beobachtet man ein gewisses „Schwingungsverhalten, aber letztendlich wird auch hier nach einer gewissen Zeit der stabile Wert von ~66% erreicht. Richtig interessant wird es erst wieder, sobald K=3 gewählt wird. Ab diesem Wert wird der Stabilitätspunkt von 66% Populationsgröße instabil und spaltet sich mit wachsenden K zunehmend in zwei Zweige auf, wobei der eine oberhalb der 66% und der andere in gleicher Weise unterhalb der 66% angeordnet ist. Diese Aufspaltung wird im Fachjargon als Bifurkation bezeichnet. Sie lässt sich in unserem Beispiel mit den Nonnen-Falter auch leicht erklären: Im ersten Jahr legen die Weibchen der Nonnenfalter so viele Eier, so dass im Sommer des Folgejahres, nachdem sich die Raupen dumm und dämlich gefressen haben und dabei der Wald zunehmend lichter geworden ist, aus ihren Puppen besonders viele Falter schlüpfen. Diese legen in der Summe noch mehr Eier und im Folgejahr gibt es dann entsprechend viele Nonnenraupen. Aber die Raupen haben nach der Halbzeit ihres Lebens nichts mehr zu fressen, da ihr Futter, die Fichten- und Kiefernnadeln, bereits alle von ihnen vertilgt sind - die Population bricht wegen Übervölkerung aufgrund der damit verbundenen Hungersnot zusammen und nur wenige überlebende Raupen können sich letztendlich zu Schmetterlingen entwickeln. Im Folgejahr wird es dann nur wenige Nonnenfalter geben und das Spiel beginnt von neuem. Die Population schwankt offensichtlich zwischen Jahren mit einer Massenvermehrung und Jahren, wo der Falter relativ selten ist, hin und her. Erhöht man in der Verhulst-Formel die Geburtenrate auf ~3,449, dann werden die beiden zuvor stabilen Werte wiederum instabil und erzeugen eine Population, die alle 4 Jahre zu einer außergewöhnlichen Massenvermehrung neigt. Und genau solch einen Zyklus kann man bei natürlichen Nonnen-Kalamitäten auch wirklich beobachten. Lässt man K weiter anwachsen, dann finden bei bestimmten Werten weitere Bifurkationen statt bis es dann irgendwann so viele sind, dass die Schmetterlingspopulation völlig unvorhersagbar von Jahr zu Jahr ihre Größe ändert (ab K=3,57). Solch ein Zustand wird gewöhnlich als „Chaos“ bezeichnet - und die mathematische Theorie, die sich mit derartigem beschäftigt, „Chaostheorie“. Wer sich den Weg in das „Chaos“ einmal als Grafik anschauen möchte, sollte im Internet einmal nach dem „Feigenbaumdiagramm“ googeln.


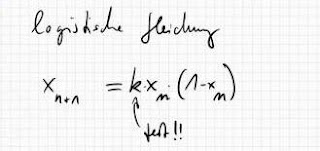


Keine Kommentare:
Kommentar veröffentlichen